Ley
de Maxwell
Forma diferencial de la ley de Gauss
Tomando
la ley de Gauss en forma integral:
Aplicando
al primer término el teorema de Gauss de la divergencia
queda:
Como
ambos lados de la igualdad poseen diferenciales volumétricas, y esta expresión
debe ser cierta para cualquier volumen, solo puede ser que:
Que
es la forma diferencial de
la Ley de Gauss (en el vacío).
Esta ley se puede generalizar cuando hay un
dieléctrico presente, introduciendo el campo de desplazamiento eléctrico 
de
esta manera la Ley de Gauss se puede escribir en su forma más general como
de
esta manera la Ley de Gauss se puede escribir en su forma más general como
Finalmente
es de esta forma en que la ley de gauss es realmente útil para resolver
problemas complejos de maneras relativamente sencillas.
Forma integral de la ley de Gauss
Su
forma integral utilizada en el caso de una distribución extensa de carga puede
escribirse de la manera siguiente:
donde Φ es el flujo eléctrico,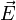 
es el campo eléctrico, 
es un elemento diferencial del área A
sobre la cual se realiza la integral, QA es la carga total encerrada dentro del área A, ρ es la densidad de carga en un punto de V
y
es
la permitividad eléctrica del vacío.
div(B) = 0 donde B es el campo de inducción magnética (Tesla)
Estas 2 leyes de Gauss junto con la ley de Faraday y la ley de Maxwell-Ampere son el grupo de ecuaciones que forman la base del electromagnetismo, llamadas las ecuaciones de Maxwell
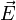es el campo eléctrico, es un elemento diferencial del área A
sobre la cual se realiza la integral, QA es la carga total encerrada dentro del área A, ρ es la densidad de carga en un punto de V
y es
la permitividad eléctrica del vacío.
Ley
de Gauss para el campo magnético
es un campo solenoidal nos dice que es la
segunda ley de GAUSS, Físicamente, por analogía con el campo
eléctrico, se puede decir que esta ley expresa que el campo magnético carece de
fuentes escalares, esto es, que no existen las cargas magnéticas (conocidas
como monopolos).
Por
analogía con el caso eléctrico, denominamos a esta ecuación Ley de Gauss
para el campo magnético.
La
ecuación sólo se ha demostrado para el
campo creado por corrientes estacionarias. Aunque la evidencia experimental muestra que es
válida siempre: para corrientes, para imanes, en situaciones estacionarias o
dinámicas. Es la experiencia la que indica que no existen los monopolos.
Para
el campo magnético la ley trata del flujo magnético a través de una superficie
cerrada es igual a la carga magnética neta dentro de la superficie, al no
existir monopolos magnéticos, la carga neta es siempre nula, y también lo es el
flujo en dicha superficie. esto se
debe porque una "carga"
magnética no es posible dividirlo en polos norte y sur, sino que siempre
estarán apareados ( no pasa lo mismo con
las cargas eléctricas que si se pueden
tener cargas + o - por separado).
La ecuación de Gauss para el campo magnético es:
La ecuación de Gauss para el campo magnético es:
div(B) = 0 donde B es el campo de inducción magnética (Tesla)
Estas 2 leyes de Gauss junto con la ley de Faraday y la ley de Maxwell-Ampere son el grupo de ecuaciones que forman la base del electromagnetismo, llamadas las ecuaciones de Maxwell
LEY DE AMPERE
La ley
de Ampère, modelada por André-Marie Ampère en
1826, relaciona un campo
magnético estático con la causa que la produce, es
decir, una corriente eléctrica
estacionaria. James Clerk Maxwell la
corrigió posteriormente y ahora es una de las ecuaciones, formando parte
del electromagnetismo de
la física clásica.
Las ecuaciones de
Maxwell permitieron ver en forma clara que la electricidad y
el magnetismo son
dos manifestaciones de un mismo fenómeno físico, el electromagnetismo.
Los
parámetros que intervienen en la formulación de las ecuaciones de Maxwell son
los siguientes:
- - Campo eléctrico existente en el espacio, creado por las
cargas.
- - Campo dieléctrico que resume los efectos eléctricos de la
materia.
- - Campo magnético existente en el espacio, creado por las
corrientes.
- - Campo magnético que resume los efectos magnéticos de la
materia.
- - Densidad de cargas existentes en el espacio.
- - Densidad de corriente, mide el flujo de cargas por unidad
de tiempo y superficie y es igual a .
- - Permitividad eléctrica, característica de los materiales
dieléctricos.
- - Permeabilidad magnética, característica de los materiales paramagnéticos.
FORMA
INTEGRAL
Siendo
el último término la corriente de desplazamiento.
Siempre
y cuando la corriente sea constante y directamente proporcional al campo
magnético, y su integral (E) por su masa relativa.
FORMA
DIFERENCIAL
Esta
ley también se puede expresar de forma diferencial, para el vacío:
o
para medios materiales:
Ley
de Faraday
Esta ley fue
descubierta por Michael Faraday en 1831, usando un diseño propio muy simple:
Al mover el imán
dentro del cartón, que tenía enrollado un alambre de cobre, las láminas
metálicas del electroscopio se abrían, indicando la acumulación de cargas
eléctricas en ambas hojuelas como consecuencia de una corriente eléctrica por
el alambre de cobre, simultánea con el movimiento. Con este experimento nos dio
a conocer que sobre el cobre recae una fuerza o campo electromagnético.
Por medio de este experimento Faraday
descubrió que la electricidad y el magnetismo se relacionaban funcionalmente si
los campos eran variables en el tiempo.
La forma matemática de
la ley de Faraday es:
Inicialmente se
creía que el campo electro era creado por la variación del mismo campo pero
magnético como si fuera el producto de
causa y efecto; ellos no tenían en cuenta que ambos campos provocaban este
cambio. Con el tiempo y los diferentes estudios y pruebas se comprobó todo lo
contrario y se empezó a implementar para mejorar la vida de las personas.
Como
resultado de todos los estudios y pruebas realizadas por Maxwell se obtuvo
estas ecuaciones, que son la base para tratar el electromagnetismo:
No hay comentarios:
Publicar un comentario